Batch 2 - Class 294 - Electric Circuits

Zoom: send meeting Id and password

Start recording

Preclass Exercise:

Attendance: Raghav, Vivaan, Aneesh, Rhea Chadha, Ryan Chadha, Adyant, Vansh, Tarush, Anika, Ayush, Shikhar, Advay, Kabir, Rohan, Dhriti, Aarav

Class Notes: (repeat from class 66)

Consider a river that consists of a trench dug connecting two lakes of equal heights. Will water flow in either direction?
What if the water height was same but one lake was deeper?
What if one lake was higher than the other?
What if we widen one of the trenches without changing its height?

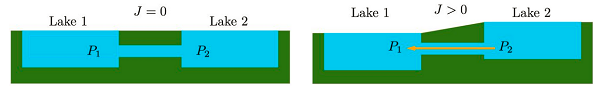
What if we increased the height difference between the two lakes? Will the flow increase or decrease?
Can we try to write the flow as function of the height difference? Lets call it push
What will happen if the trench had a lot of rubble in it?
What if the trench was made really smooth?
Can we try to write the flow as a function of the resistance in the trench?
Arrive at the relationship flow=push/resistance

Why does lightning happen? (Difference in charge - accumulated electrons)
What happens in lightning? (charge flows trying to equalize the electric potential)

Just like water needs a trench to flow, electrons need a conductor to flow - "closed circuits"
What do you think would happen to the flow if there was a lot of difference in charge?
What do you think would happen to the flow if the wire the conductor wasn't as good?
Can we try to write the flow (current) as a function of difference in charge (potential difference) and resistance?
Voila! We just discovered Ohm's Law!
Units of potential difference, current and resistance are volt, ampere and ohms, such that 1 V = 1 A & 1 Ohm

Exercise - Suppose a floor lamp with resistance of 5 Ohm required a current of 70 A to properly function. What is the potential difference that must be applied?

If there are three resistors in series to a battery, what is the total resistance and current?
Lets think back in terms of trenches - if there are three trenches along the way, what can we say about the flow through each?

Overall, should there be more flow than one trench or less?
What would be the potential difference across each trench
What is the sum of these potential differences? (say similar to sum of height differences?)
Now can we arrive at a way to connect individual resistance to overall resistance?

Same concept applies to circuits - current through each resistor must be the same, and hence R = R1 + R2 + R3
Note that voltage across each resistor is different, and sum to those is the total voltage difference

Think about it as an electron moving, gaining kinetic energy due to voltage difference, and then losing some of it going through the resistor - In a full cycle, it must gain as much as it lost

If there are three resistors in parallel to a battery, what is the total resistance and current?
Lets think back in terms of trenches - if there are three trenches in parallel, what can we say about the flow through each?

Overall, should there be more flow than one trench or less?
What would be the potential difference across each trench, and flow through them?
What is the sum of these flows?
Now can we arrive at a way to connect individual resistance to overall resistance?

Same concept applies to circuits - voltage across each resistor must be the same, and hence 1/R = 1/R1 + 1/R2 + 1/R3
Note that current through each resistor is different, and sum to those is the total current
What will happen if you connect many electric devices in parallel?

Homework

References: